DIY Atmospheric Optics Experiments
Leonardo's cross caustic: a complex composite light pattern
Leonardo's cross is a term that may be used for the complex composite light pattern observable below floating surface bubbles. Several mechanisms are at play to each produce distinct features or components of the composite light pattern: cusp caustics, fold caustics, an astroid caustic and sharp borders produced by aperture effects. By a detailed study of decomposable/filterable scatter plots obtained using a custom-written 3D raytracer, each features' corresponding mechanism can be deduced. The figures below depict the outcome of such an analysis, where the subscripts denote the interaction (T, transmission; R, reflection) with any of the 3 interfaces: o: outer meniscus, i: inner meniscus, c: cap (part of a sphere).
These and many more results have been submitted to Applied Optics and are currently under peer review.
Note how even details such as the Tc Ti Ro-cusps internal structure (red half-circle feature missing from the tip of the just-forming cusp) due to the onset of total internal reflection (TIR) visible at the shown screen-distance. (Simulation parameters: R_0/a=100, Gamma=75°, z_0 = H_infty - 0.8*r_b, with r_b being the bubble radius, H_infty the water level at infinity, R_0 being the inner bubble meniscus radius of curvature at the bottom, and a the capillary length of about 2.7mm for water)

For larger distances of the screen below the bubble upon which the light is cast, the astroid will be more fully developed with 3 cusps present. The last cusp to appear is typically the left-pointing one towards the incidence light direction. (Simulation parameters: R_0/a=100, Gamma=75°, z_0 = H_infty - 3.5*r_b).
For even greater depths relative to the bubble size the two left-pointing cusps (towards the light incidence direction, i.e. the Tc Ti To To- and the Tc Ti Ro-cusps) can be observed to become visibly offset on the symmetry axes. In the particular image below, they appear to coincide in their cusp points.
Note also, how the partial astroid caustic (3 cusps developed, the left-pointing is missing up until very large depths for shallow light inclinations / highly oblique incidence) is "magically" completed/complemented by the two left-pointing cusps to give a false impression of a single complete astroid caustic.

Demonstration experiments for atmospheric optics phenomena exists abundantly. Nonetheless, the web also proliferates myths and at times does not lay emphasis on a correct physical explanation in favour of vivid expositions of phenomena such as rainbows. Diffraction experiments (e.g. using a CD-R) or simple dispersion by a wedge of water often substitute true physical analog experiments. The resulting displays often do not resemble the actual phenomenon, e.g. diffraction "rainbows" show a pure spectrum whereas the colored rainbow caustic really is a mixture of colors (a superposition). By contrast, there exist also beautiful and physically more faithful experiments which demonstrate for instance rainbows or halos using only very simple means. Below you will find setup schematics for a few selected long-known experiments (i.e. Florensce's rainbow, Bravai's spinning prism) as well as new experiments such as the analog refraction halo experiments. These and similar experiments are analyzed quantitatively in the following publications:
- "Wine glass caustic and halo analogies", M. Selmke, Applied Optics (Appl. Optics) Vol. 57(19), 5259-5267 (2018)
- "Revisiting the round bottom flask rainbow experiment", M. Selmke and S. Selmke, American Journal of Physics (Am. J. Phys.) Vol. 86(1), 14 (2018)
- "The rainbow in the box", M. Selmke and S. Selmke, American Journal of Physics (Am. J. Phys.), Vol. 86(4), 316-318 (2018)
-
"Artificial Circumzenithal and Circumhorizontal Arcs", M. Selmke and S. Selmke, American Journal of Physics (Am. J. Phys.) Vol. 85(8), 575 (2017)
- "Artificial Halos", M. Selmke, American Journal of Physics (Am. J. Phys.), Vol. 83(9), 751-760 (2015)
The props necessary to do the experiments sketched below and many more on atmospheric refraction phenomena can be either obtained individually (e.g. purchasing on e-bay round-bottom flask or other glassware, acrylic beads etc.), or inexpensively in math toy geometric solid sets (see also note in "physics at home" section).
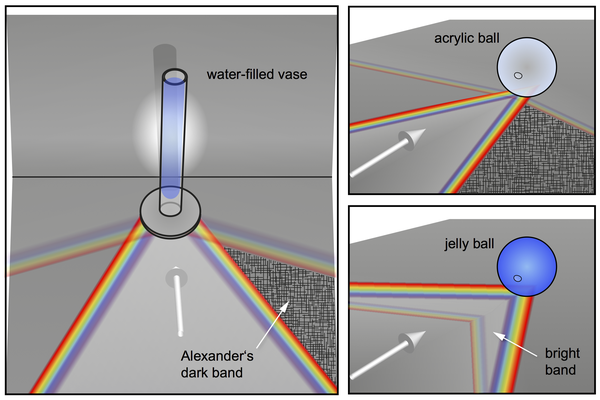
Florence's rainbow experiment refers to the century-old model raindrop experiment in which a water-filled globe (spherical flask, i.e. a Florence flask) is illuminated by white & parallel light through a hole in a screen. Such experiments were already made in the 14th century by Theodoric of Freiburg and later by Descartes (Lés Météores, 1637). If the screen is far enough away, even Alexander's dark band may be observed. If the screen is rather close to the flask the secondary rainbow will still be inside the primary bow. Splitting of rainbow orders may be observed and is due to the glass wall.
Using a long cylindrical water-filled vessel (e.g. a vase), one may experimentally reproduce the first and second order rainbows fairly easily. In addition, Alexander's dark band may be visualized more easily by inclining the incident light direction (whereby the effective index of refraction is tuned, according to A. Bravais' theory of refraction of inclined rays).
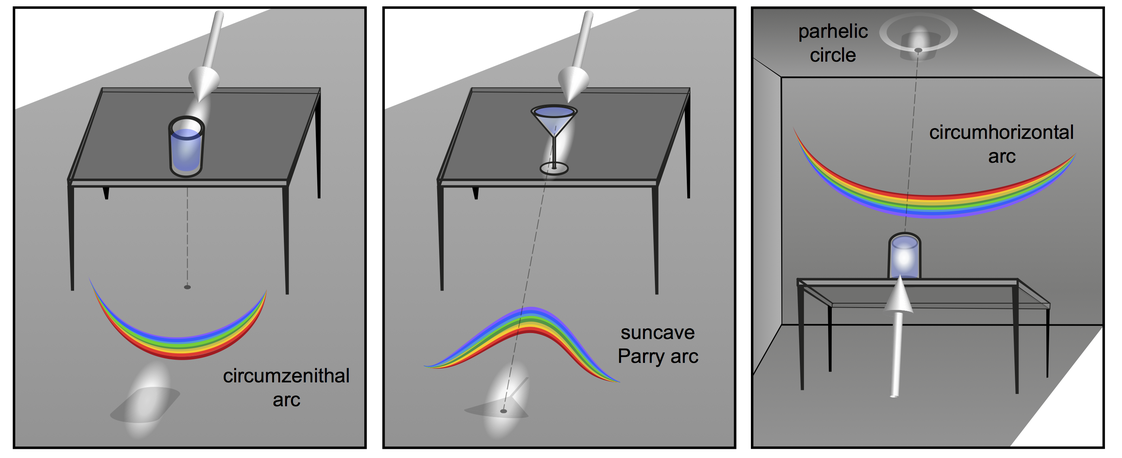
Some special ice halos may be reproduced faithfully using water-filled vessels or glasses as well, see the article "Artificial Circumzenithal and Circumhorizontal Arcs" (downloadable under publications). Specifically, illuminating a cylindrical water-filled glass or a V-shaped cocktail glass (Martini glass) one may reproduce the circumzenithal arc (CZA) and circumhorizontal arc (CHA) or the suncave Parry arc, see below. These experiments produce pure spectra, provided that the distance of the projection surface is far enough away from the glasses. For the CZA the illumination angle must be shallower than 32°, whereas for the CHA the illumination must be very steep from below.
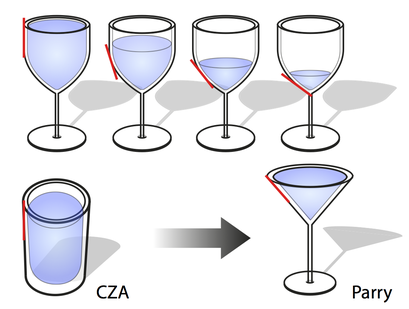
Using a wine glass of the specific form as shown, and using different filling levels, one may tune an artificial projected halo from the circumzenithal arc (a circle segment around the point below the glass) to a suncave (with respect to the glass shadow) upper Parry halo. The reason being that the rays which contribute to the halo will predominantly experience a second refraction which will have the right inclination angle of the interface, being somewhere between a vertical second interface or an inclined interface as for the Martini cocktail glass. I.e., this experiment combines the CZA and the Parry halo experiments without requiring two different glasses. More on this: "Wine glass caustic and halo analogies", M. Selmke, Applied Optics (Appl. Optics) Vol. 57(19), 5259-5267 (2018).
(There are also so-called filling bodies available for ideal experiments: A google-search for "View-Thru geometric solids" / "clear geometrical solids" / "3d shapes Volume Set (fillable)" / "geometric volume / shape set" (in German: search for "Mini Füll-Körper") gives a good variety of liquid-fillable shape sets which typically contain a hexagonal prism (for parhelia & other halo phenomena), a cylinder (for analog circumzenithal / circumhorizintal halo experiments), a equilateral triangular prism (for parhelia experiments) and a cone (for analog Parry halo experiments) amongst others.)
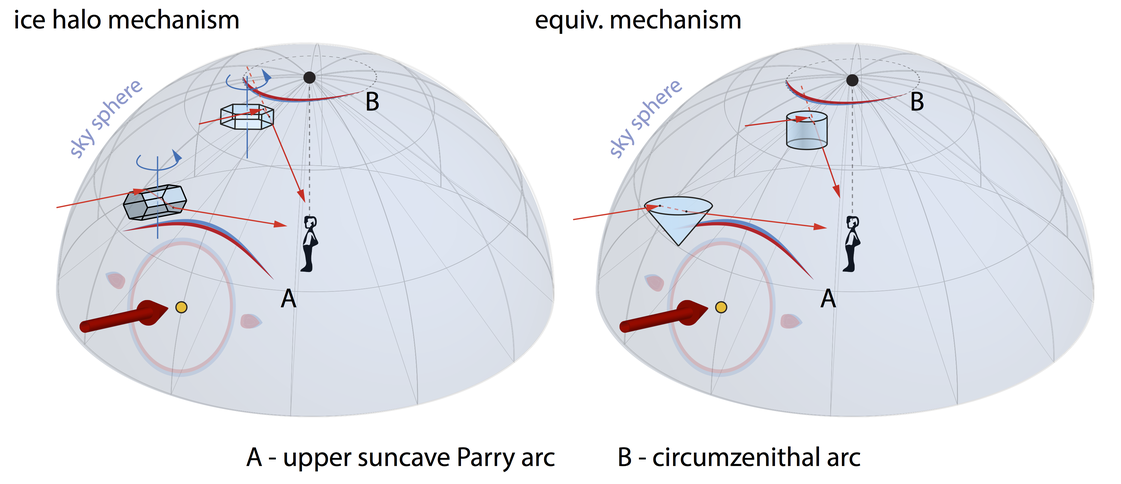
The general idea of the equivalence as atmospheric-phenomena-generating objects between simple geometric bodies and halo-forming (rotationally sampled) ice crystals can be sketched and understood by the following sketch. But it must be kept in mind that only the prismatic hexagonal ice crystal represent the true physical mechanism in the atmosphere which cause the natural halo phenomena, though the simpler bodies would also cause virtually indistinguishable phenomena were they to exist e.g. in cirrus clouds. Importantly, they allow the reproduction of the natural phenomena at home (see experiments above).
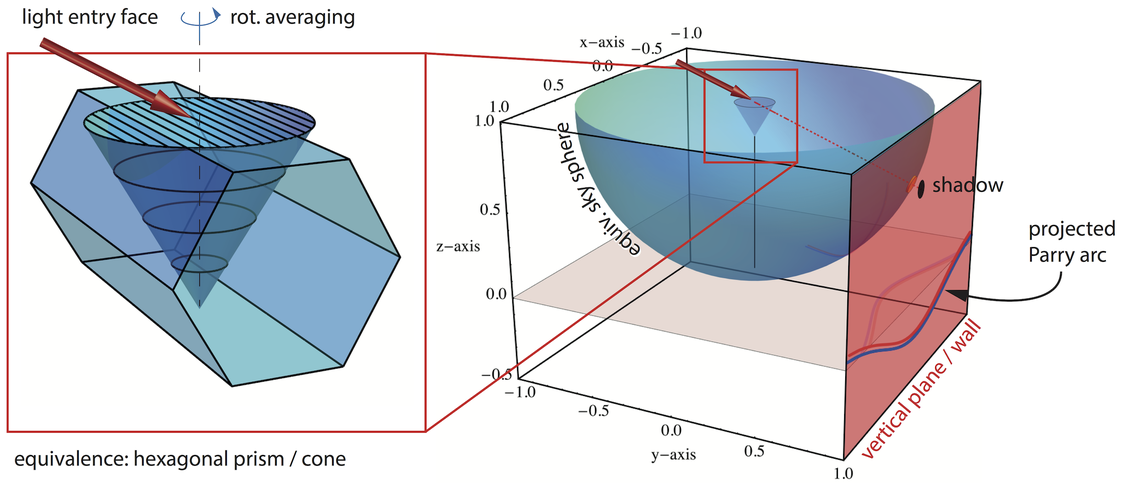
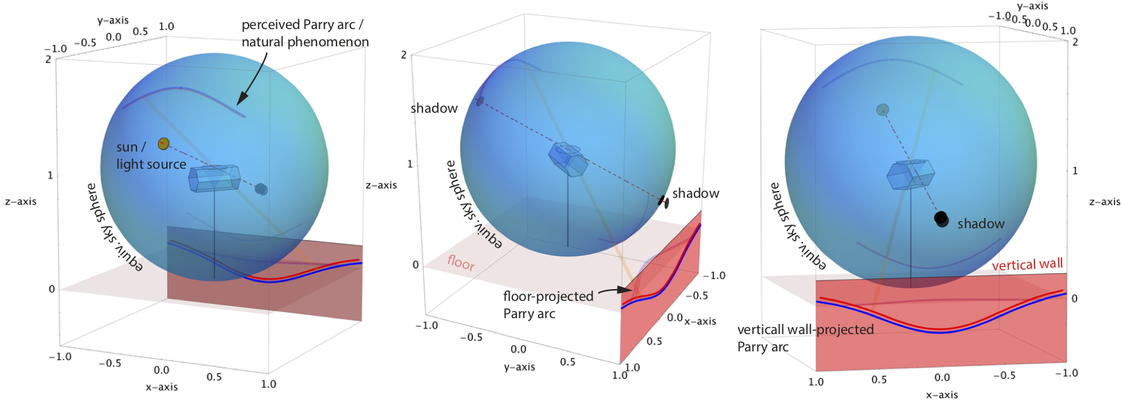
The following sketch illustrates the experimental situation and the various projections of the artificial (upper suncave) Parry arc, either on the wall (vertical xz-plane) or the floor (z=0-plane / xy-plane / horizontal plane). The xy-plane experimental projections correspond to gnomonic projections of the halos, i.e. projections from the sky sphere's center to the plane tangent at the nadir. The equivalence between the refraction through a 60° cone and the refraction through a hexagonal prism (incl. rotational averaging of the latter) through the appropriate faces is also illustrated on the left.
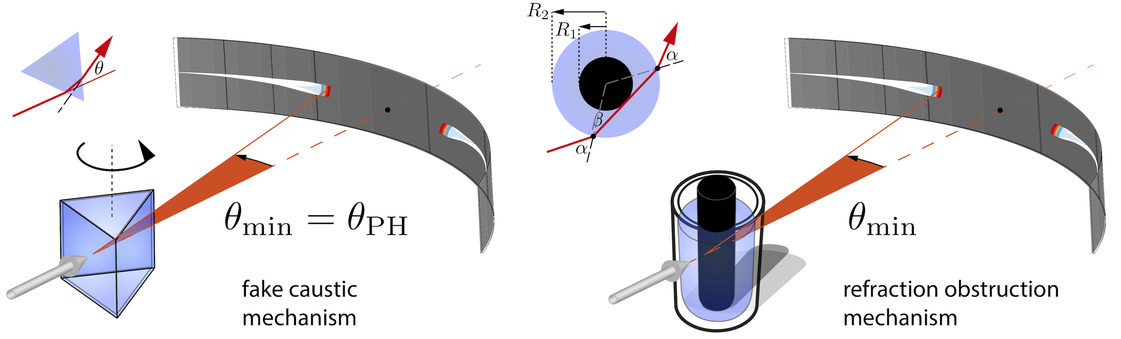
An experiment to recreate parhelia consists in rotating an equilateral prism or a hexagon about its symmetry axis. Upon illumination a fake caustic emerges. This faithful demonstration experiment was first done by A. Bravais in the 19th century. The parhelia angle of minimum deviation through an A=60° prism at zero solar (or light source) elevation is θ_PH=22°=2*ArcSin(n*Sin(A/2)) - A, cf. "Artificial Halos", M. Selmke, Am. J. Phys. 83(9), 751 (2015).
Following instead the idea of Huygen's (false) mechanism for parhelia, one may perform a simpler experiment which still rather closely recreates the appearance of the 22° parhelia (sundogs). The geometry required to achive the same minimum deflection angle (θ=2*(α-β)) through the water glass with a central obstruction is R_2/R_1=2, as we have shown in the footnote [39] of "Artificial Circumzenithal and Circumhorizontal Arcs", M. Selmke and S. Selmke, Am. J. Phys. 85(8), 575 (2017). The deviation angle θ through a water glass is a monotonic increasing function of the impact parameter. The obstruction causes the minimum deviation to be non-zero (as it would be for a central impact with no obstruction), and the tuning of the radii such that R_1=R_2/2 achieves that the minimum deviation is 22° instead. However, the intensity distribution is different as the mechanism is not equal to the parhelion's fake caustic mechanism which involves a local minimum in the deflection function of the prism as a function of the prism orientation. The overall appearance is nonetheless quite similar!

A few fun experiments I have done in the past years are summarized below. On the image you see me working on the custum-built confocal microscope setup which was used in one way or another for almost all experiments I did on photothermal physics. The upper microscope objective collects the light transmitted through the sample (metallic square plate mounts the sample glass-slides on the piezo table fixed in the upper stage breadboard) and focuses it on the two photodiodes.
Optical Tweezer Setup
The following setup was designed to trap and observe microscopic particles.
Photonic Rutherford scattering
This macroscopic demonstration experiment visualizes the concept of photothermal microscopy.
The experiment and its analysis is described in detail in my article "Photonic Rutherford scattering: A classical and quantum mechanical analogy in ray and wave optics", M. Selmke and F. Cichos, American Journal of Physics, June 2013, Volume 81, Issue 6, pp. 405.

The physical principle which lies behind photothermal microscopy is a lens-like effect of the refrative index gradient that s created around a heated particle. In this macroscopic demonstration experiment, a large (1cm) metal sphere was embedded inside a transparent resin cube (5cm x 5cm x 5cm). The thermal expansion that accompanies the laser heating of the sphere by a 2W focused green laser beam into a small hole of the sphere results in a refractive index profile which has a characteristic 1/r dependence on the distance r to the center of the sphere. The same type of refractive index profile is generated in photothermal microscopy around an absorbing nanoparticle of a few nanometers size, i.e. 10^(-9) m. One may then observe either a deflection of a probing beam (red ray in the image), or see the lens-like symmetric warping around the sphere (imgage below).
Similar to the mirage effect which reflects grazing rays of light through the heated air above an asphalt surface on a hot day, the inhomogeneous optical density of the medium around the sphere acts like a lens. Thereby, a characteristic warping of anything viewed through the cube can be seen. In ths experiment, a digital camera took a picture of a square lattice pattern positioned about 20cm behind the thermal lens medium, while the camera itself was positioned about 30cm in front of the cube. The resulting images of the pattern as taken by the camera through the medium are shown below. Without heating (blue) and a few seconds after 10 minutes of heating with 2W.
The Green Flash
Inspired by the wonderful article "A simple experiment that demonstrates the green flash" by Johannes Courtial in the American Journal of Physics, this experiment recreated the elusive and rare so-called "green flash", an optical atmospheric phenomenon in which the setting sun sometimes appears green just before it disappears behind the horizon. A fishtank filled with water simulates the Rayleigh-scattering of the atmosphere while the wedge-like shape of the tank acts like a prism whereby the dispersion of light by the air of the atmosphere is also simulated. In combination, a white light source can appear green seen through the tank. The image taken seen below taken with a digital camera shows an array of high-power LEDs seen through the tank. The further right the columns get, the more greenish the left-most part of the dispersed LED spectrum becomes. The milk effectively scatters out the blue part first, leaving the green to remain.